Using Python to Graph 3D Vector Calculus Objects in Blender 3D

– – Personal project for graphing mathematical objects from vector and multivariable calculus on Blender 3D’s built-in python script feature.

You will need Blender installed. This script was written in the 2.79 version. It should work for the current 2.8 version. Paste the code onto Blender’s script mode.

Since Blender is 3D, this software can only support mathemtical objects up to 3 dimensions. Blector can support the following classes:

Multivariable functions of 2 variables, under class name “MVF”
Planes, under class name “Plane”
Vector-valued functions, under class name “vvf”
Paths (Simple Vector functions of t), under class name “Rt”
Vector Fields, under class name “Vector_Field”
Gradients, under class name “Gradient”
Any class in the script that aren’t mentioned above aren’t meant to be graphed.

Rules for string representation of functions:

Most functions will be represented by strings that get evaluated with python’s eval function. When representing variables in string, “@” is used for x, “!” for y, “$” is used for z. Using non-alphabet symbols is just to prevent collision with math functions that also have the same letter. These correspondences are not arbitrary; you must use “@’ for x, and so on.
For better clarity, use parentheses as much as needed
if your function strings ever use exponentials, please enclose the value being exponentiated in parenthesis,
```
e.g. write "(@)**2", not "@**2".
```
Mathematical functions and constants will use python’s math class
Example: 2x + y^2 + sin(z) + pi + e + ln(x) + sqrt(y) + sec(z), will look like this in string form:
```
"(2*@) + ((!)**(2)) + (math.sin($)) + (math.pi) + (math.e) + ((!)**(.5)) + (1/(math.cos($)))"
```

Rules for graphing:

All created math class objects must be called by the function “make” after creating the object, which is how its information will be graphed visually onto Blender.

- Graphing multivariable functions (MVF):

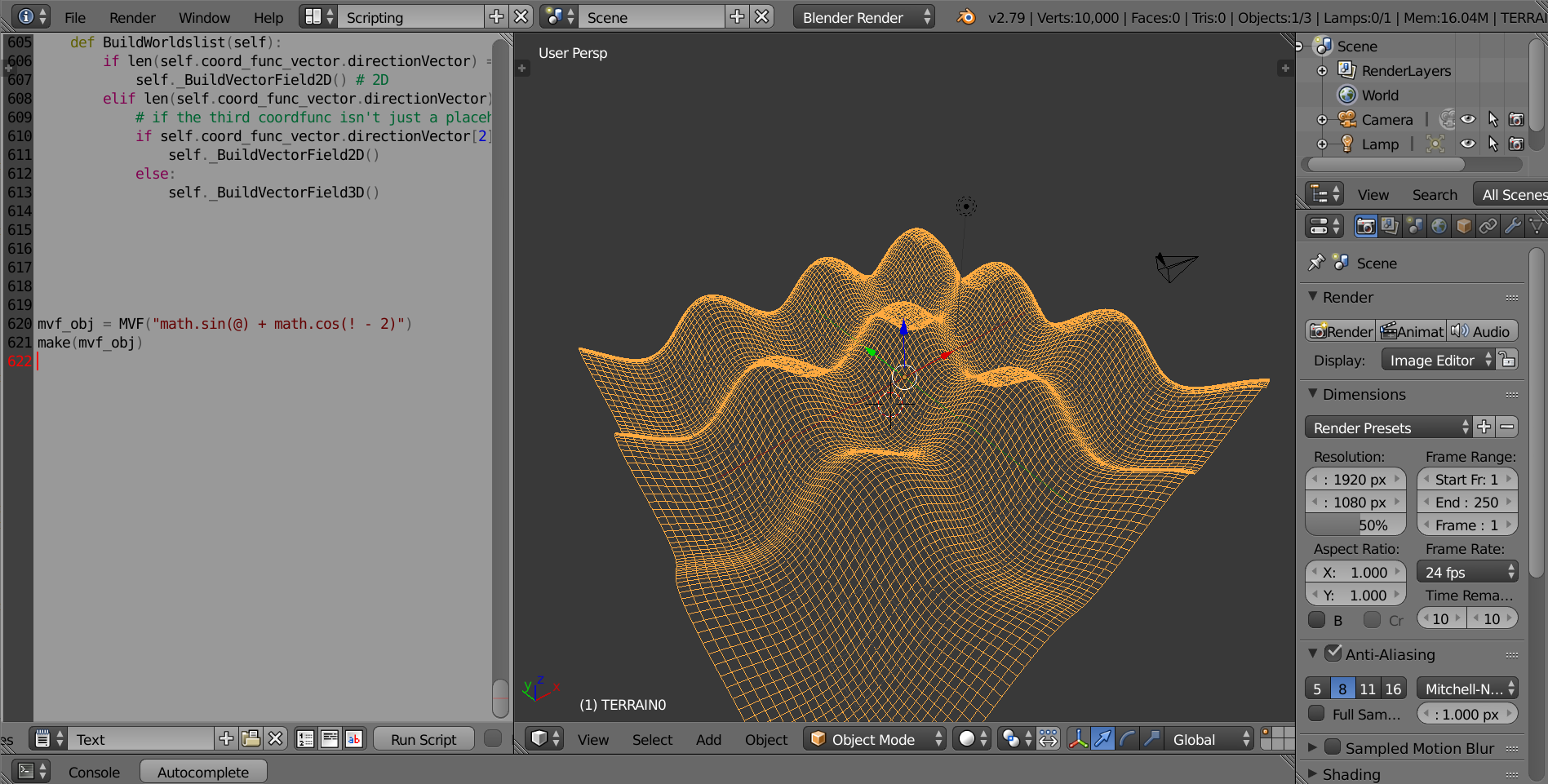
Write the function as a string, where “@” is for x, “!” is for y. MVF can only support 2 variables, so z is not possible. Example code: # graphing the function f(x, y) = y^2 - x^2

mvf_obj = MVF("((!)**(2))-((@)**(2))")
make(mvf_obj)

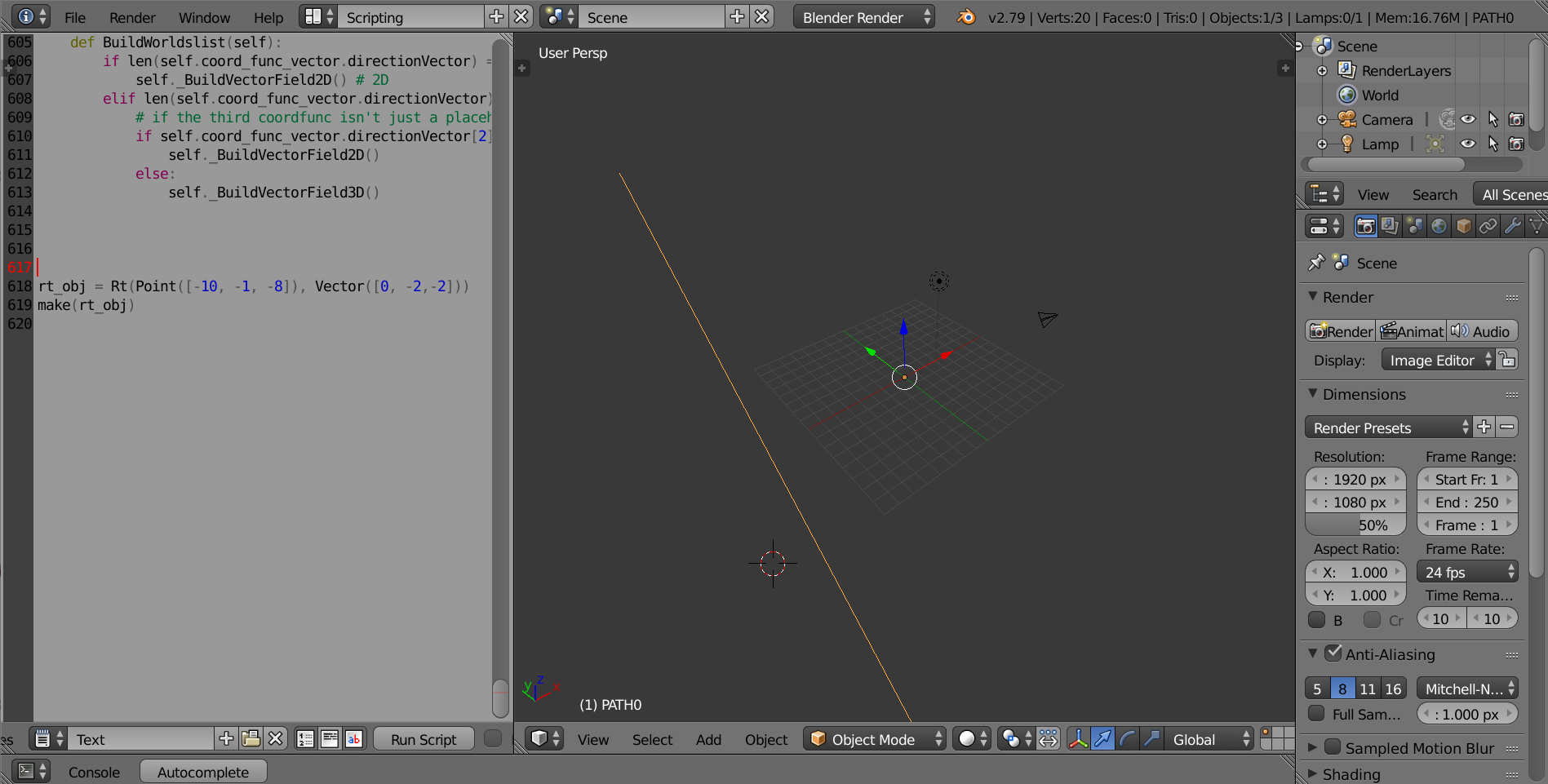
- Graphing Paths (Rt):

(Supplemental Class: Vector, Point) Create the Point object for the origin or base point, and the Vector for the direction vector. Example code: # graphing R(t) = (-10, -1, -8) + <0, -2, -2>

rt_obj = Rt(Point([-10, -1, -8]), Vector([0, -2,-2]))
make(rt_obj)

Rt can be used to graph vectors in general. To do this, make the Point the origin, and set optional argument asVector to True when creating the object. Example code: # graphing the vector <-4, -4, 8>

rt_obj = Rt(Point([0, 0, 0]), Vector([-4, -4, 8]), asVector = True)
make(rt_obj)

- Graphing Vector-valued functions (vvf):

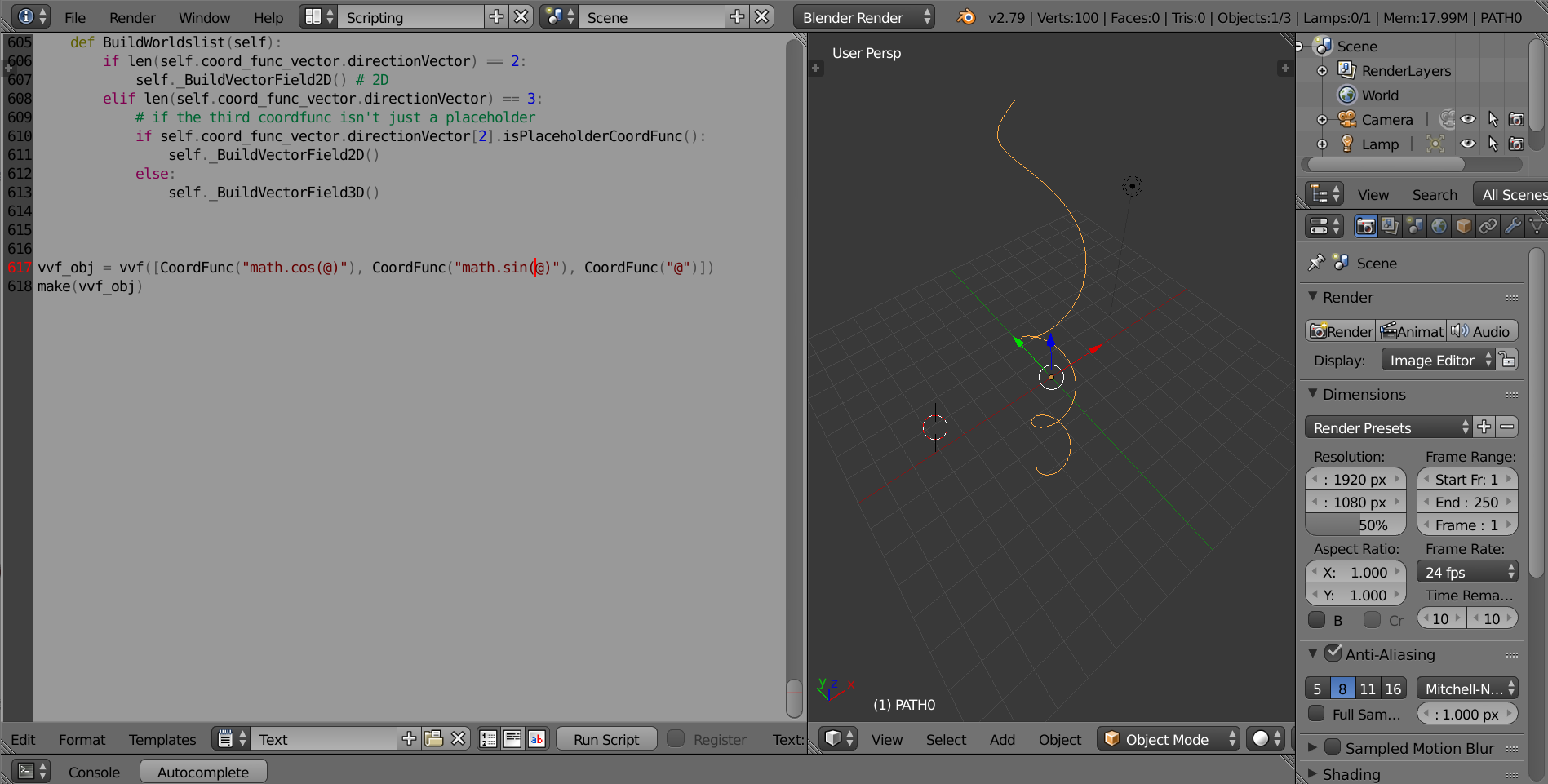
(Supplemental Class: CoordFunc) Write a list of CoordFunc objects that are all in terms of “@” (which will be the “t” in regular vector valued functions). The list must have length 3. If you do not want to have a 3rd component, use the placeholder CoordFunc(“0”) for the 3rd item. The vvf class by itself is usually for 1 variable (t or “@”) in its components. For vector-valued functions with multivariable coordfuncs, see Gradient and Vector_Field. Example code: graphing r(t) = <-cos(t - 2), sin(2t)> (or -cos(t -2)i + sin(2t)j)

vvf_obj = vvf([CoordFunc("-math.cos(@ - 2)"), CoordFunc("math.sin(2*@)"), CoordFunc("0")])
make(vvf_obj)

- Graphing Gradients (Gradient):

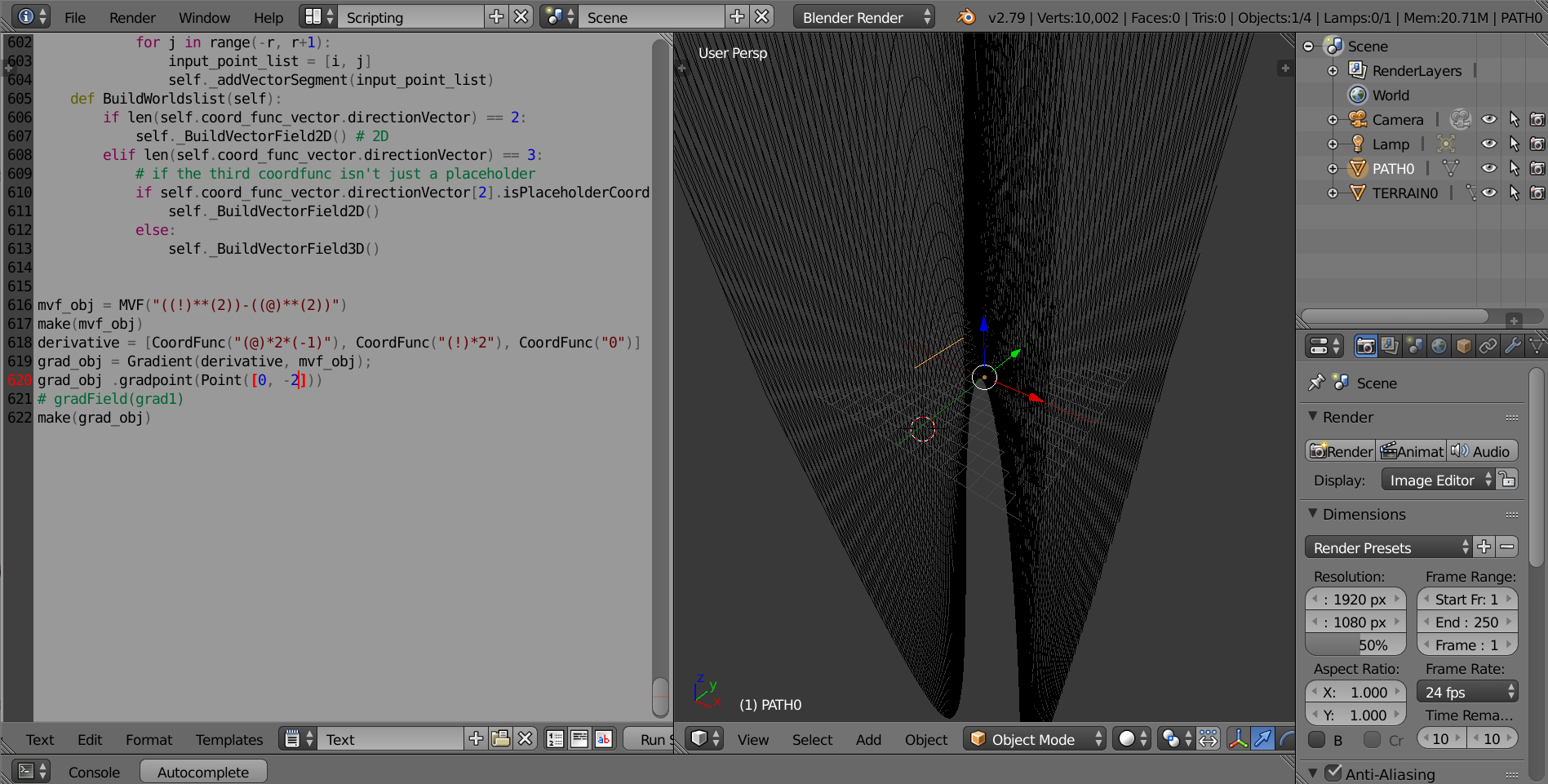
(Supplemental Class: vvf, MVF, Point) You will need the original multi variable function as mvf, and then the derivative of the MVF as a vvf, and a point to signify the base point for the gradient vector You can also avoid implementing the basepoint in the initial creation, and install it later with the function gradpoint, but do so before calling make(). T The result is a vector on the MVF, pointing towards the direction of steepest ascent. Example code: Graphing gradient of f(x, y) = y^2 - x^2 at (0, -2)

mvf_obj = MVF("((!)**(2))-((@)**(2))")
make(mvf_obj)
derivative = [CoordFunc("(@)*2*(-1)"), CoordFunc("(!)*2"), CoordFunc("0")]
grad_obj = Gradient(derivative, mvf_obj);
grad_obj .gradpoint(Point([0, -2]))
# gradField(grad_obj)
make(grad_obj)

- Graphing Vector Fields (Vector_Field)

(Supplemental Class: vvf) Create a vvf withe the multivariable CoordFuncs, then create the Vector FIeld object with it Example code: graphing F = <-xy, y, 0>

vvf_obj = vvf([CoordFunc("-@*!"), CoordFunc("!"), CoordFunc("0")])
vector_field_obj = Vector_Field(vvf_obj)
make(vector_field_obj)

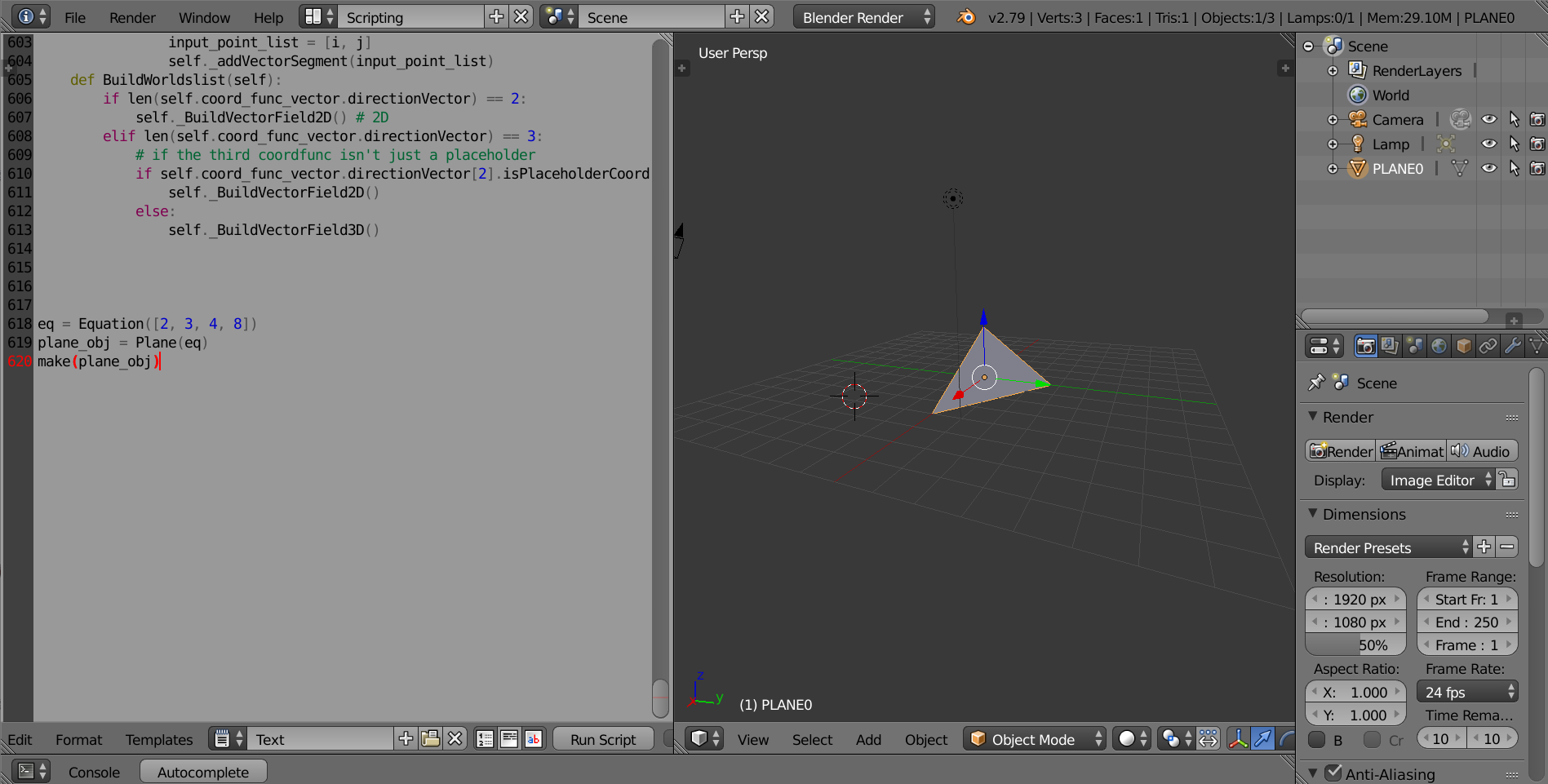
- Graphing Planes (Plane):

(Supplemental Class: Equation, Vector, Point) There are 2 ways to create the Plane class: A) With a plane equation in the format of ax + by + cz = d (Recommended) Write a list of 4 real numbers. This is basically the [a, b, c, d] from a plane’s standard form of ax + by + cz = d. Initialize the Equation class with it. Example code: # graphing 2x + 3y + 4z = 8

eq = Equation([2, 3, 4, 8])
plane_obj = Plane(eq)
make(plane_obj)

B) With the normal vector and a point Write the normal vector and the base point Example code: # normal vector is <2, 3, 1> and point is (1, 2, 3)

plane_obj = Plane(Vector([2, 3, 1]), Point([1, 2, 3]))
make(plane_obj)

Supplemental Classes:

Point: Used by Planes, Rt, Gradient, for being base points usually.
Vector: Used by Planes, Rt, for normal vectors and direction vectors respectively
Equation: Used by Plane, to represent the standard form ax + by + cz = d
CoordFunc: Used by vvf, represent the component functions of a vector valued function (vvf)
Field: parent object for Vector_Field
Blector: the central class in which all math objects are processed through when make is called on it.

Example Images

Multi-variable Function (MVF)
Rt being used to graph a vector.
Path (Rt)
Vector valued Function (vvf)
Gradient (in orange) at one angle. MVF (in black) is also graphed for reference.
Same Gradient (in orange) at another angle for clarity. MVF (in black) is also graphed for reference.
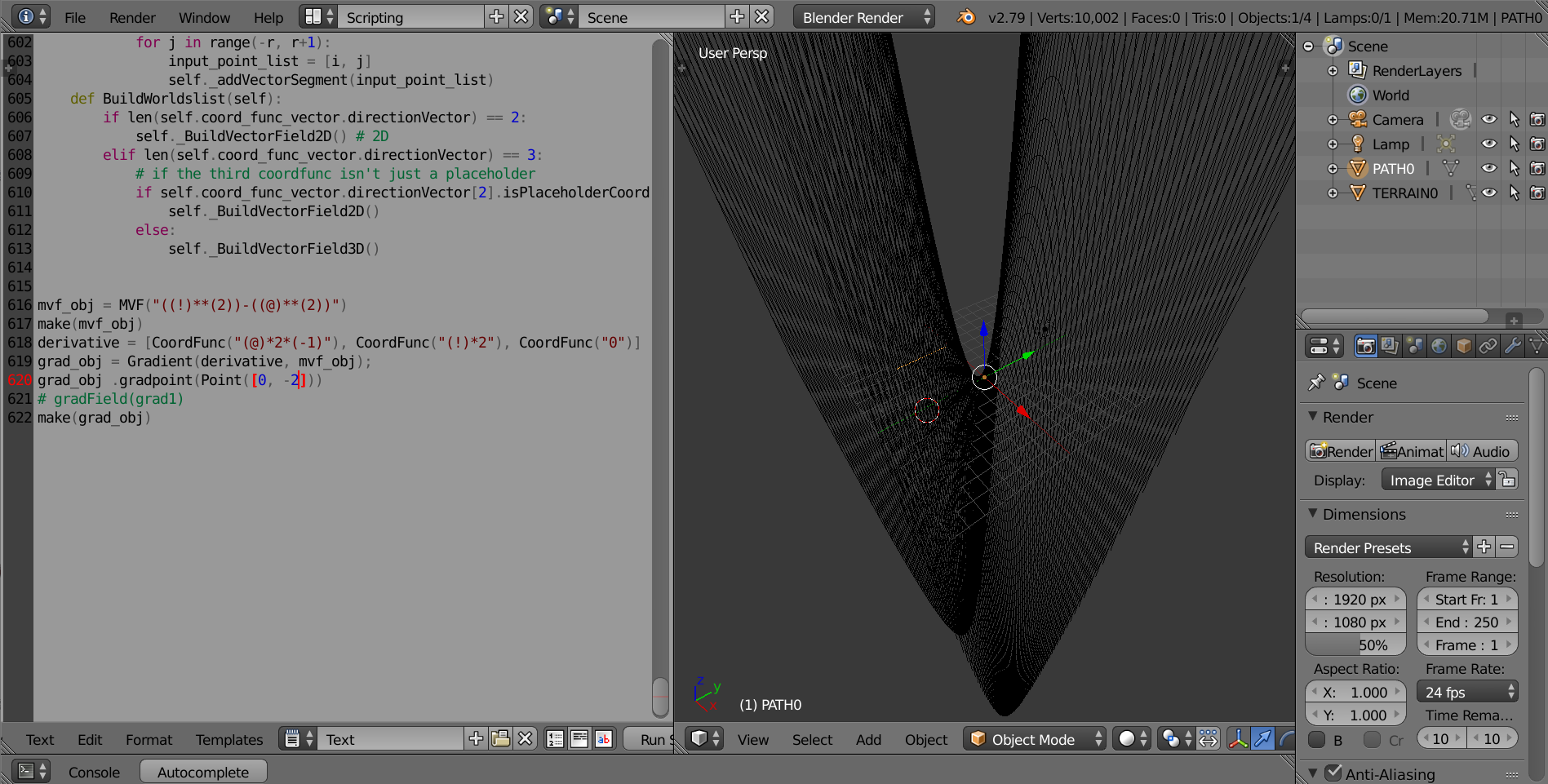
Gradient Field of the same gradient from before (gradField)
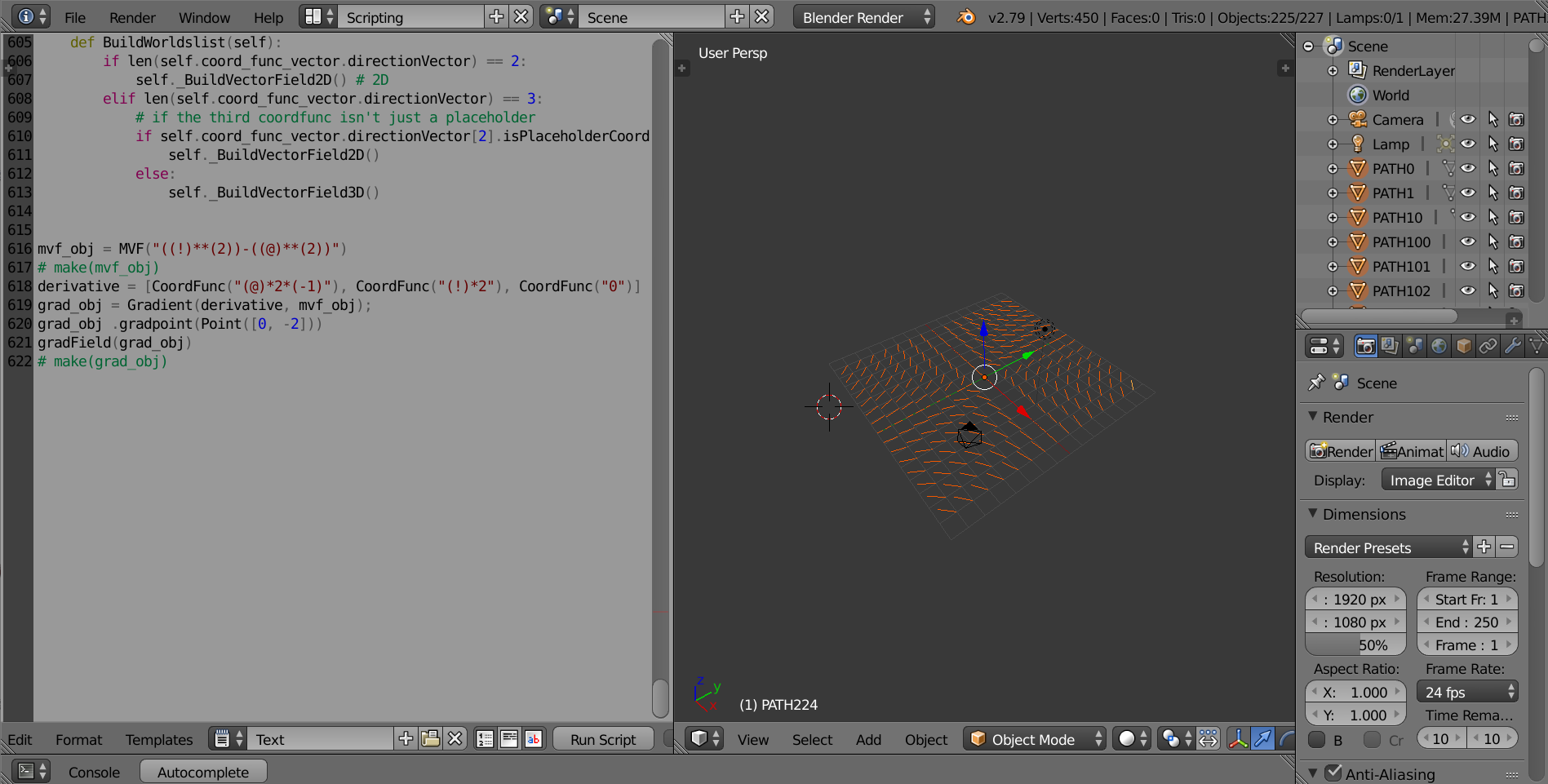
Vector Field (Vector_Field)
Plane (method 1 with equation)
Plane (method 2 with normal vector and point)